Welcome to Monalisa’s documentation!

First of all, why should you use Monalisa?

1. Monalisa targets non-Cartesian reconstructions, motion-resolved/motion-corrected reconstructions, and partial Cartesian reconstructions. It offers great tools especially for radial imaging and motion-resolved/motion-corrected reconstructions. These are the best use cases for the current toolbox.

2. Monalisa is easy to install and well documented – as you can see!

3. Monalisa is great for learning non-Cartesian iterative reconstruction methods.

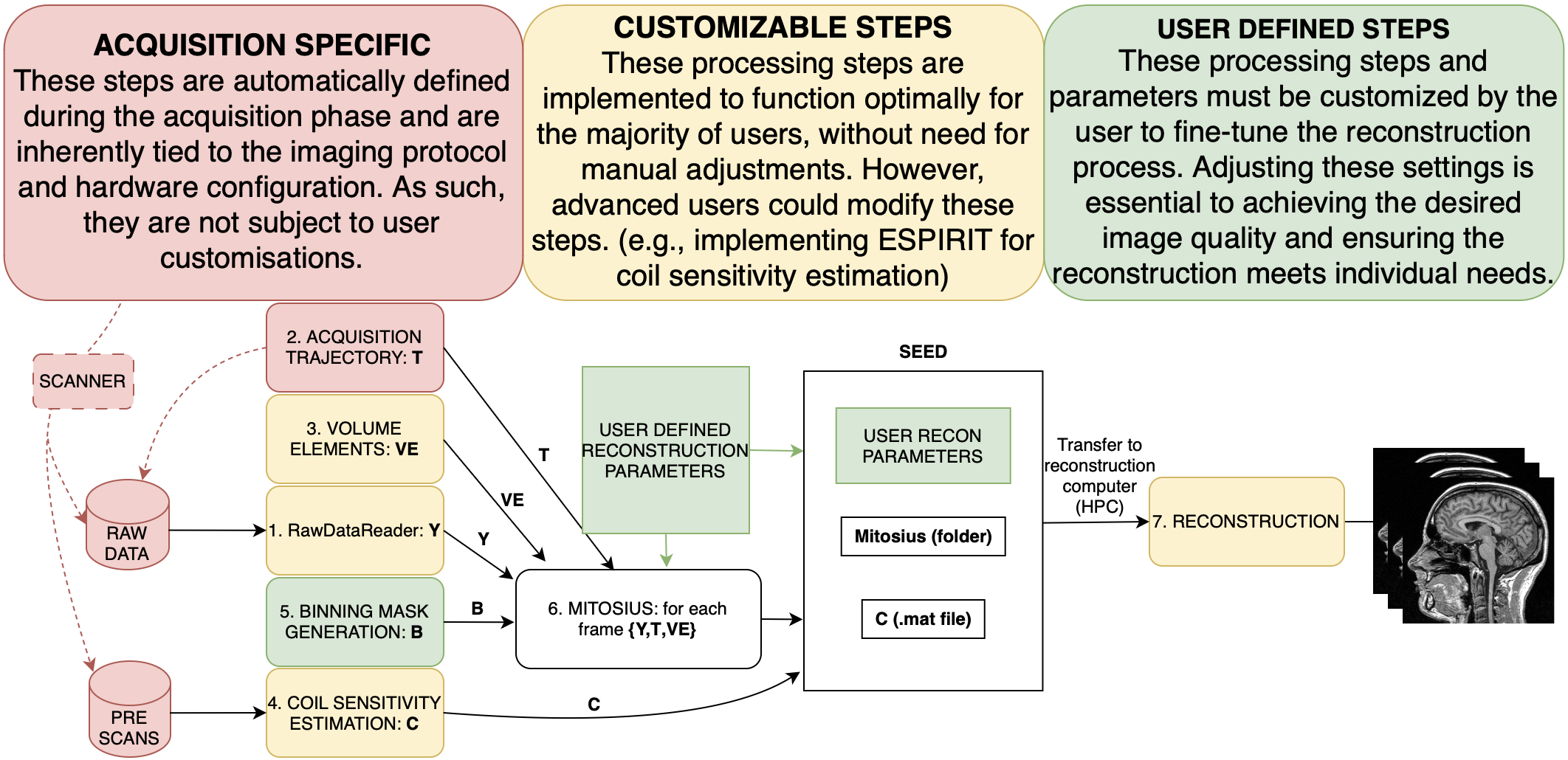
Here you can see a simplified schematic of the pipeline in Monalisa. Information from the acquisition raw data files is processed through multiple stages, together with additional information, such as the trajectory, volume elements, and user-defined binning and reconstruction parameters. Colored blocks indicate the degree of user control: red denotes acquisition-specific steps that are fixed and cannot be modified after acquisition; yellow highlights configurable steps that are rarely changed but can be customized or improved; green represents user-defined steps that must be adapted for each reconstruction. Initially, the workflow defines binning masks alongside coil sensitivity estimation and volume element computation. This is followed by the mitosius preparation, and finally, image reconstruction. The sections below are explaining each step extensively. Need more help? Consider opening a GitHub issue on our repository.

• Quick Start
  • Hello Monalisa
  • Installation
    • Clone the Repository
    • Set Up a c++ Compiler
    • Add Monalisa source path to your MATLAB path
    • Compile the C++ Source
    • Verify Installation
    • Notes
• Contents
  • Introduction
    • The Design of Monalisa
    • A few Definitions
    • A Quick View at the List of our Reconstructions
  • Reconstruction Calls
    • Input Arguments for Reconstruction Functions
    • Non-Cartesian Static Reconstructions
    • Deformation-Fields
    • Non-Cartesian Chain Reconstructions
    • Non-Cartesian Sheet Reconstructions
    • Partial-Cartesian Static Reconstructions
    • Partial-Cartesian Chain Reconstructions
  • The Mitosius
    • Prerequisites
    • Usage instructions
    • Notes
  • Binning: Flexible Readout Rearrangement
    • First Example: Sequential Binning
    • Second Example: Task-Based (Hi-Fi) fMRI
    • Third Example: Respiratory Binning for Motion-Resolved Cardiac MRI using Superior-Inferior (SI) Projections
    • Fourth Example: Cardiac Binning for Motion-Resolved Cardiac MRI using Superior-Inferior (SI) Projections
  • Coil Sensitivity Map Estimation
    • Coil sensitivity from pre-scan images
    • Coil sensitivity from raw data pre-scans
    • Automated Estimation
    • Manual Estimation
    • Code Explanation
  • Acquisition Guidelines for Coil Sensitivity Estimation using Prescans
  • Volume Elements or Density Compensation
    • What are Volume Elements? Basic Usage
    • Ok, but why are there Volume Elements?
  • Trajectory Definition in Monalisa
    • What is a Trajectory? Basic Usage
    • Custom Trajectories
  • Reading Raw Data
    • Basic Usage
    • Advanced Details for Developers
• Examples
  • Tutorial 1: Reconstruct MRI rawdata
    • Step 1: Compute Coil Sensitivity
    • Step 2: Binning
    • Step 2.1: allLines Binning - A Single Bin
    • Step 2.2: Sequential Binning - 5-Second Temporal Bins
    • Step 3: Preparing the Data for Reconstruction (Mitosius)
    • Efficient Workflow: Local Preprocessing, HPC Reconstruction
    • Step 4: Running Reconstructions

• API

• Docker for Monalisa
  • Dockerfile Setup
  • License Requirements
  • Steps to Run Monalisa
• Acknowledgment and Authors
  • Cite the Article
  • Reference the Repository and SOPs
  • Contact for Significant Advancements or Commercial Use
    • The contributors behind Monalisa
    • Acknowledgements
• Discussion
  • Sketching a Classical Thermodynamic Theory of Information for MRI Reconstructions
    • Introduction
    • Iterative Reconstructions
    • The Phase Space
    • The Space of Memory States
    • The Heat Engine
    • The Computer as an Engine
    • A Postulate for the Thermodynamical Entropy of the Dynamic Memory
    • Information and Efficiency
    • Connection with the Theory of Information
    • Parallel Computing
    • Connection with the Landauer’s Principle
    • Connection with Statistical Mechanic
    • Artificial Intelligence as an Amplification of Efficiency
    • Conclusion

↑